換水 - Peri's Hobby

Periの雑多なホビー活動の記録

水換えの目的は、ある期間Tに飼育水中に蓄積する不要物を取り出すことであると考えます。
老廃物としては、濾過バクテリアによる分解の生成物である硝酸イオンや水草が吸収しきれなかったリン酸イオンなどがあります。これらの老廃物は、Tの間に水槽に投入される餌やTの間に溶出する底床肥料などが発生源になりますから、魚や水草を飼育・育成する以上発生源を絶つことは事実上不可能と考えるべきでしょう。
水換え不要をうたう商品は、硝酸をバクテリアの力で分解しガスとして放出することで蓄積しないようにするという仕組みになっているように見受けられます。

現実解として換水が不可避だとしたときに、どれくらいの頻度でどれくらいの量を行えば良いのかが問題になってきます。
セオリーとしては週一回1/3とか1/4とか言われますし、全量換水は危険といわれますが、その根拠は不明です。
換水によってバクテリアが減少するという論もありますが、濾過が効いている水は濁りも無いですから水中にバクテリアが大量に生息しているとは考えられません。バクテリアは濾材に居るから濾過が効くのであって、水を換えてもバクテリアは減少するとは考えにくいです。

そこで、定期的に換水を行うものとして換水率を換えたときに水の変化がどうなるか、計算してみました。

換水期間 : Δt
換水回数 : n
経過時間 : T = ΣΔt = Δt・n
n回目の換水までの期間 : tn
Δtに蓄積する老廃物(溶質)の量 : s
換水率 : p
換水前の飼育水中の老廃物総量 : Sb
換水後の飼育水中の老廃物総量 : Sa
n回目の換水前の飼育水中の老廃物総量 : Sbn
n回目の換水後の飼育水中の老廃物総量 : San

としたときに、
Sbn = Sa(n-1) + s (1回前の換水からΔt経過し、s分の老廃物がたまる)
San = Sbn・(1-p) (換水によりpが新水になるので、残る古い水は(1-p)、pは新水なので老廃物は0)
となります。

Δt = 1,s = 1, Sb0 = 0としてpを変化させたときの様子をn = 25まで表計算ソフトを使って計算させた結果のグラフを載せました。
ある一定期間が経過すると、Sb = 1/p、Sa = 1/p - s に収束します。

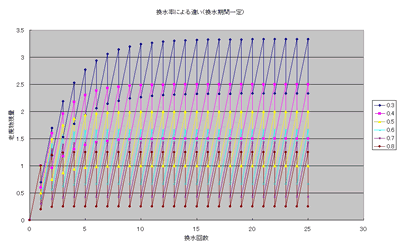
この結果から

1. 換水率にかかわらず、換水前後での水中の老廃物の変化量は同じ。Sb - Sa = s
2. 換水率の大小により、水中に残る老廃物の量は変わる。双曲線関数なので、換水率が0.5(半量換水)より少ないと、残る老廃物の量は急激に多くなるが、0.5より多くしても残る老廃物はあまり減らない。
3. 換水による老廃物の量の変化率は、Sa/Sb = 1-psとなり、pとsが小さいほうが少ない。

がわかります。

水換えが水槽環境に与える影響を考えた場合、次を考える必要があります。
A) 藻類対策などのため、老廃物の総量を低く保つ必要がある
B) 老廃物が存在する環境に馴れた生体には、老廃物の変化率が大きいと悪影響がある

A)を実現するには換水率は高いほうがよいが、B)のためには換水率が低いほうが良いということになります。
ところがBは比率の問題なので、換水前の老廃物の総量が十分少なければ、新水と飼育水の差異が少ないですから影響は小さくなるし、総水量に対する老廃物の割合の問題(sは濃度で考える)なのでsが十分小さければpの値の影響は小さくなります。

このことから、週一回1/3換水というセオリーは否定されます。
１．藻類が出ないようにするためには、一回の換水率を多くする(pを大きくする)
２．水量が少ない場合は頻度を高く(sを小さくする)
３．魚が多い場合は餌も増えるので頻度を多く(sを小さくする)
必要があることがわかります。
また、餌を入れすぎたとか緊急で水質を元に戻す必要がある際には、1/3換水を繰り返しても意味は無く、1回での大量換水が必要であることがわかります。これは、Sbが極端に大きくなった状態から定常状態に戻るまでの回数を考えればわかります。また、こういった状況に対応するためにも、飼育水は新水に近い状態に維持したほうが安全であるように思います。

FirstUpload 09/11/15-22:10 : LastUpdate 09/11/15-22:10